Welcome to Global Journal of Urology

Abstract

The Bayesian concept is complex and contrary to intuition, but it is fundamental in the practice of medicine as well as in biotechnological development. We expect that a tragedy of ignoring the Bayesian concept will result clear to the reader who should acquire the tools to recognize its meaning, as well as, its use; but especially, to visualize the serious consequences of ignoring it. The physician is not mystically fascinated for knowing what percentage of patients who has prostate cancer have no symptoms (47%), urinary frequency (38%), urinary urgency (10%), decreased urine stream (23%) or hematuria (1.4%). What the physician and every patient want and vitally need to know is the probability of having prostate cancer, giving that he has one or more of those symptoms.

Keywords: Medical Errors; Iatrogenic disease; Sensitivity and specificity; Diagnostic Techniques and procedures

This is a pervasive tragedy, apparent trivialities that cost lives with the combination of neglecting Bayesian theorem and producing categorical medical error. On a conceptual basis, everything said here applies isomorphic ally to all screening diagnostic methods.

According to the National Cancer Institute at the National Institutes of Health:

Prevalence of prostate cancer: In 2016, an estimated 3,110,403 men were living with prostate cancer in the United States [1]. Since there are out of 158,380,000 males in the US, the prevalence is 1 out of 50 males [2]. With such prevalence of prostate cancer, if the physician sees a patient with a > 4 ng/ml positive prostatic antigen, then he has a decisional problem harder than it seems.

For the sake of a model concept, let’s say that for an arbitrary artificial intelligence (A.I.) system in an airport, one out of three pregnant women have an under-detected pregnancy, in the sense that a screening procedure (observation while walking, at two meters distance, the AI system cannot detect pregnancies of the first trimester). In a subpopulation subjected to this screening procedure, the true prevalence of pregnancy would be the number of diagnosed plus half this number, which is slightly counterintuitive. Out of 9,000 pregnant women taken randomly, approximately 6,000 would be considered pregnant by the A.I. system. (6,000 plus 3,000).

The Bayesian concept is complex and contrary to intuition, but it is fundamental in the practice of medicine as well as in biotechnological development. Our Bayesian manifest constitutes the determination to eliminate much of iatrogenic effects and other serious consequences of this type of selective prebilaterian innumeracy in health sciences [3-5]. We expect that a tragedy of ignoring the Bayesian concept will result clear to the reader who should acquire the tools to recognize its meaning, as well as, its use; but especially, to visualize the serious consequences of ignoring it [5].

The ideas contained here surely confront the beliefs and intuition of the medical community and, for this reason, can give the false impression that it is an opinion or a controversial topic, however, it constitutes a rigorous application of science and mathematics [6-10] to health problems, medical education and biotechnological development [3]. It is not implied an axiological stance from the authors, because if the reader thinks the implications are terrible or uncomfortable, "horrible dictum “, the authors thoroughly agree; however, by acknowledging the horrible, nothing is refuted. We also present it in strict adherence to what we consider the ethical responsibility of medical writers.

In general, most physicians understand the phenomenon of medical negligence that becomes medical malpractice when the doctor’s negligent treatment causes injury to the patient and iatrogenic. The side effects and risks associated with the medical intervention are called iatrogenesis. Hence, iatrogenic ailments are those where doctors, drugs, diagnostics procedures, hospitals, and other medical institutions act as “pathogens” or “sickening agents”[11]. Almost all physicians believe that they understand the cause of medical negligence and iatrogenesis. We doxastic ally maintain that the doctors who believe so are wrong.

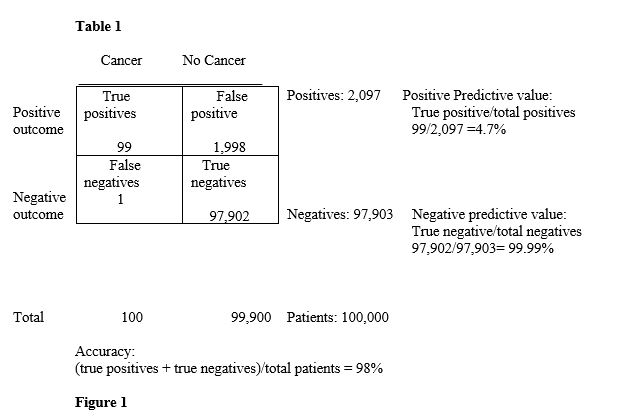
The Socratic method, we must remember, is composed of two parts: the first is destructive, refutative and confrontational of false beliefs; nevertheless, necessary. It is characteristically represented by the irony that consists of refuting and exhibiting the ignorance of the apparent sage and it is called elastics. Serving to refute; applied to indirect modes of proof and opposed to deictic. The second part is creative and positive and is the art of what today corresponds to statistical inference and it is called heuristics or maieutics [12]. When someone has preconceptions that prevent analysis, then elastics is used, conveniently, as a method and this is one procedure that we use here [12]. We can stage a hypothetical example of the Bayesian tragedy. The data are intended for pedagogical purposes and in no condition as a real instance: “Sorry, you have cancer! With an expression of consternation and great empathy, the doctor gives this diagnosis to a 50–year- old woman, with no abnormal clinical data, who underwent a screening procedure, designed for a subpopulation of her age. For this hypothetical type of cancer, the test sensitivity is 99%, the specificity of the test is 98% and the prevalence of the disease is one out of 1,000 women in the subpopulation to which the patient belongs. If we tentatively suppose the scene is true, what probability would the reader assign to the patient as having cancer? [5]. For the peacefulness of many, we should mention that the vast majority of physicians assign a probability of around 95% [5].

In one classical study, they asked 20 residents, 20 students in the last year of medical school and 20 medical specialists, selected from meetings in hallways in four teaching hospitals of the medical school at a highly prestigious university. The majority of doctors give the same wrong answer to this problem, usually, around 15% answered correctly [13]. If the reader follows carefully the process, with a calculator at hand and makes annotations respectively, may follow each step without difficulty; In addition, to extend this analysis, anyone can review lessons on Bayes Theorem in our channel Principia Pedagogical, Eléntica, Heuristica [14-17]. As one out of 1,000 women in this subpopulation has this hypothetical type of cancer; if we choose randomly 100,000 patients, around 100 would have the disease.

Since the test has 99% sensitivity, it correctly diagnoses 99 out of 100 patients who have cancer; If we put these 100,000 patients to the test, only 99 (100 times 0.99) of the 100 who have cancer will be correctly diagnosed as positive, which are the cases called true positives. The patient to whom test resulted negative, only one in this case, (100 minus 99), but actually has cancer, is a false negative.

Of the 100,000 patients that were so put to the test 99,900 (100,000 minus 100) do not have cancer. Since the specificity is 98%, so only for 98% of the non-diseased patients the test is going to be negative, which means 97,902 (99,900 times 0.98) are the true negatives; the 1,998 (99,900 minus 97,902) remaining patients, who do not have cancer, are false positives; that is, 2% of healthy patients, since the test correctly diagnoses 98% of healthy patients, which means that it errs in 2% of the cases, giving them falsely positive (99,900 times 0.02).

To know how accurate the test is, we have to use an arithmetic fraction’s sum of true positive, added to the true negatives all divided by the total of patients that were tested. It corresponds to 99 of the true positives plus 97,902 of the real negatives. All divided by 100,000 patients, that is, the accuracy (exactitude) of the test is 98% ((99 + 97, 902) /100,000), which should not be confused with the probability that the patient has cancer. The set of all positive patients is comprised of true positives, which means 99, plus false positives which are 1,998; a total of 2,097.

The probability that a patient has cancer, given that the test was positive, is the so-called positive predictive value; which means the true positive (99) divided by all positives (2, 097), which equals 4.72%. This means that in the case analyzed here, the probability that a patient has cancer, given that the test was positive, is less than 5%, that is, if this test is positive, most likely (95%) the patient does not have cancer.

The set of all negative patients is constituted by the true negatives (97,902) added to the false negatives (only 1), which gives a total of 97,903. True negatives that are 97,902 divided by all the negatives who are 97.903 is equivalent to 99.99%. The probability that a patient does not have cancer given the test was negative constitutes the negative predictive value. This means that if the test was negative, the patient has a 99.99% chance that she does not have cancer.

We have all heard the expression from the doctor's mouth and sometimes from our own: "The results do not seem correct to me; they need to be repeated in a reliable laboratory".The description of the disease is done by setting the percentage of patients who have the disease and who also have determined signs, symptoms, laboratory results, etc., as discussed in the Current Medical Diagnosis and Treatment 2016, in its Fifty-fifth edition [18]; however, in the reality of medical practice, the clinician encounters a patient who has symptoms, signs, laboratory´s results. The physician should question himself over the probability that the patient has the disease the doctor supposed. To answer this, the Bayes theorem is always required and thus avoid the risk of iatrogenesis, occasioned when conditional probability is ignored. Millions of patients can be saved scandalously, unexpectedly, and somewhat counterintuitively only by the simple application of Bayesian statistics. Thus, we can show the existence of statistical iatrogenesis, caused by false-positive results, erroneously interpreted as equivalent to disease.

Perhaps the reader could become convinced of the compulsory incorporation of Bayesian analysis to every health program. Statistical ignorance sickens and kills by mixing reality with the dream of increasing the sensitivity of the tests as if sensitivity could be an objective on itself and thus quality becomes a mortal enemy. Each day that passes without implementing Bayes' theorem to the clinical procedures, thousands of healthy people around the readers of this article suffer and die.

Even the best courses for medical education, such as Kaplan [19], fall into the problem and, sometimes, in more profundity, as seen as in a case brought in the course of epidemiology relative to screening tests in a case with hypothetical data, in approximately the following terms:

A 55-year-old man visits his doctor due to an increase in urinary frequency, decreased urine stream and hematuria. During the physical examination, a nodule of a diameter of one cm. is found in the prostate gland. The doctor prescribed a test of serum prostate-specific antigen. Let´s accept that a level greater than 4 ng/ml is considered abnormal. Using this standard, this test has 67% sensitivity and 97% specificity. Suppose that an epidemiological article published recently found that in a cross-sectional study, 10% of the men in this group of age have prostate cancer. The result of this patient's specific prostate antigen is 7 ng/ml. What is the best estimate of the probability that this patient actually has prostate cancer? [19].

For the analysis detailed of this kind of problems, in particular, the reader is referred to our channel Principia Pedagogical, Eléntica, Heurística [14-17].

https://www.youtube.com/channel/UCuOndmIcw2GbdiGdccDXtBQ 

The prevalence, for this subpopulation, of prostate cancer, from the given epidemiological data is 10%, that is, one in 10 patients of this subpopulation has prostate cancer. Then about 10,000 out of 100,000 men randomly chosen in this subpopulation has cancer. The sensitivity of the test is 67%, so out of every 100 patients with cancer, only 67 are correctly diagnosed as positive. If now, we test those 100,000 patients, only 67% of the 10,000 patients who have cancer will be correctly positive, which means, true positives are 6,700 (10,000 times 0.67) and the other 3,300 (10,000 minus 6,700) patients are false negatives, because even though having cancer, the test was negative on them.

The specificity of the test is 97%, that is, out of every 100 patients without cancer, 97 are correctly diagnosed as negative. Then out of the 90,000 (100,000 minus 10,000) patients that does not have cancer, only 97% is going to have a negative test, i.e., true negatives are 87,300 (90,000 times 0.97) reporting 2,700 (90,000 minus 87,300) patients without cancer with a positive result, i.e., 3% of patients who do not have cancer are false positives.

The accuracy of this test is the result of the sum of the true positives, plus the true negatives, and the sum divided by the total number of patients who were tested. Corresponding to 6,700 of true positives added with 87,300 of the true negatives all divided by 100,000 patients, it is equivalent to 91.3%. The set of all positive patients consists of true positives (6,700) plus false positives (2,700), in total 9,400. The probability that a patient has cancer, given that the test was positive, is the so-called positive predictive value; i.e., true positives (6,700) divided by all the positives (9,400), which equals 71.3%. This means that in the case analyzed here, the probability that a patient has cancer, given that the test was positive, is close to 70%, This is the answer to which the educator arrives; however, it is incorrect, as explained below. The set of all negative patients consists of true negatives that are 87,300 added to the false negatives that are 3,300, giving a total of 90,600. True negatives (87,300) divided by all the negatives (90,600) equals 96.4%. The probability that a patient does not have cancer because the test was negative constitutes the negative predictive value. This means that if the test was negative, the patient has a 96.4 % chance that he does not really have cancer.

The conclusion reached by the medical expositor is incorrect, but, in this case, not because of mathematical error, but because the patient was not discovered as part of a screening process application, since the patient went to the clinic with a florid clinical picture. The determination of sensitivity and specificity was performed in people who had no manifestations of the disease and not in those who arrive at the clinical office with a change in urinary frequency and a palpable nodule in the prostate. This phenomenon is called a categorical error. The patient does not belong to the subpopulation without manifestations. Therefore, the instructor underestimates the diagnostic probability of disease.

The reader does not need to go far to find out about the significance of Bayes' theorem. This has such an impact that it is recognized as fundamental in the clinical diagnosis in the first chapter of the nineteenth edition of Harrison’s Principles of Internal Medicine, a chapter, so fundamental that is written by the editors [4]. At present, and according to the same nineteenth edition of Harrison 's Principles of Internal Medicine, in its third chapter, it is recognized that unfortunately there is no perfect diagnostic tests. After each test is performed, the true disease state of the patient remains uncertain. The quantification of residual uncertainty is done using Bayes' theorem that provides a simple way to calculate the probability of a disease after obtaining the result and this is done from three parameters, the prevalence of the disease in the subpopulation to which the patient belongs, the sensitivity and specificity of the test itself [20].

As an extremely representative unintentional misleading information example, as appears in Medscape [21]:

Prostate Cancer Diagnosis and Staging

Signs and symptoms:

With the advent of PSA screening, patients report the following local symptoms:

• No symptoms (47%)

• Urinary frequency (38%)

• Urinary urgency (10%)

• Decreased urine stream (23%)

• Hematuria (1.4%)

As a physician you are not mystically fascinated for knowing what percentage of patients who has prostate cancer have no symptoms (47%), urinary frequency (38%), urinary urgency (10%), decreased urine stream (23%) or hematuria (1.4%). What you and every patient want and vitally need to know is the probability of having prostate cancer, giving that he has one or more of the following signs: no symptoms, urinary frequency, urinary urgency, decreased urine stream or hematuria. A Christmas incident is pertinent: A boy is told that 99% of Santa Claus impersonators are dressed in red; notwithstanding, the clever boy wants to know what is the probability that a person dressed in red is a Santa Claus impersonator. He may not want to waste his time asking for presents to a cardinal of the Catholic Church. As expressed by Laplace since 1795, even though probability calculation is generally against intuition, it constitutes an essential part of the application of mathematics to science and health problems, medical education, as well as to the courts [3,22-24]. The decision-making by the physicians has to be based on evidence, so that patients derive broad full benefit from the available scientific knowledge. The formulation of differential diagnosis requires, not only a broad base of knowledge, but also the ability to determine the relative probabilities of each disease given certain sign, symptoms or laboratory parameters and not vice versa [20]. Several quantitative tools are essential to synthesize the available information, including diagnostic tests and the Bayes theorem.

Diagnostic tests from a cell blood count to a study of the highest technological sophistication such as synchronized positron emission tomography (GATED-PET) [25] serve to reduce the uncertainty related to the diagnosis or prognosis and help the physicians decide the best diagnosis. The accuracy of a particular test is obtained using sensitivity (true positives) and specificity (true negative) as well as the positive and negative predictive values. Bayes' theorem uses information about the sensitivity and specificity of the test in conjunction with a-priori probability of a diagnosis, which is represented by the prevalence in the subpopulation under study, to determine the post-test probability, that the patient has the disease in question [20]. This is probably the most important concept that physicians should have and its ignorance, indifference, and disregard constitute a tragedy in education and in the application in clinical medicine, as well as in the technological development [5]. Beyond the tragic epistemological consequences, the informed consent or informed authorization of patients, is meaningless when it is not a product of the application of Bayes' theorem and this has, increasingly, legal implications, both civil and criminal which must have terrified to the part of the medical world that disregards or ignores these fundamental concepts [3]. The development of biotechnology is determined by the demand of doctors and patients that focuses on increasing the sensitivity of diagnostic tests, disregarding specificity, increasing false-positive results and the social, emotional and economic costs associated with this phenomenon [3]. Calling the expert in statistics when the study is done is absurd, it is already too late; in the same way, to call biotechnologists to perform what the physician considers necessary is to destroy the huge resources the biotechnology has. To ask the biotechnologist to develop certain diagnostic test or produce a drug with genetic engineering, without the application of Bayes' theorem to the problems is to proceed as the worship of the machine [24].

It is an unnecessary complication to convert a continuous variable into a discrete variable and then convert it into a Boolean variable, which often gives rise to the assumption that diseases are discrete entities that either the patient possesses or does not. The majority of diseases are continuous states, arbitrarily discretized and then converted to Booleans. It consists of taking a Manichean’s stand, with the tendency to reduce reality to a radical opposition between good and evil, between health and illness.

This way of proceeding, wearing the mathematical clothing and attributing the condition of hypothesis to what is nothing more than a hypostasis is exemplified in the Bayesian tragedy. Additionally, the error of seeking confirmatory evidence instead of refutative evidence is, as Popper demonstrated, contrary to scientific proceeding [26]. The foregoing is, in part, a consequence of the way in which the various instances mistakenly proceed, where each instance verifies the result of the previous one. Science acts in the opposite direction. Each instance must have totally different procedures, which in strict logic should agree in the results. In science, this is called consilience. Ideally, the results obtained with any method should demonstrate the existence of the same nosologically entity as the other methods have done. If a radiological study discovers a tumor, this should, ideally, be consistent with the results obtained in ultrasound, in Computed Tomography, in positron emission tomography, in Nuclear Magnetic Resonance, in a biopsy, in an endoscopic or laparoscopic study, in diverse biochemical studies, etcetera [3,27].

If clinical medicine would consist of verifying if a study was done well, it would be unrecognizable comparatively with witchcraft. This is the main reason for which the second opinion patients ask for, do not produce what is expected. The patient does not understand the Bayes theorem, and frequently neither his own physician. We propose the obligatory incorporation of Bayesian analysis to any health program in the world. Bayesian ignorance makes healthy people sick and kills many of them, in the hands of fanatics of increasing the sensitivity of tests.

One of the main causes of morbidity and mortality in the world is iatrogenesis, which is as we have said of any alteration of the patient's condition produced by the doctor, prescription drugs or diagnostic procedures and their misinterpretations. In the case described with prostate cancer we are not talking about wrong results, but about misinterpretations, which we can divide into those of a medical nature and those of a Bayesian nature. Apophenia is a false perception of patterns or missing links from random events or meaningless data. In statistics, apophenia corresponds to a type I error, while Pareidolia is a phenomenon of hyper -recognition of patterns, from a vague and random stimulus perceived wrongly as an identifiable shape. It is a pseudo salience of Thom’s “catastrophe theory”. So, pareidolia is a type of apophenia [24,28-35]. For the wise reader, to which this paper is destinated, in this case, the medical student, Bayes Theorem is not anymore, a conspiration of the shadow of a phantom wandering in the hospital, but an instrument, he has acquired, to tame conditional probability and to avoid a pervasive tragedy. Here it is, Bayes’ theorem in the general formulation, as difficult, powerful and apotheotic as it looks:

D_e = Disease

A = Affirmative test

D_j = healthy

P(• ) = Function of Bayesians Probability

If A is any affirmative (positive) test with

positive probability, such that $\mathrm{A}\subset \underset{\mathrm{e}\in \mathrm{J}}{\cup }{\mathrm{B}}_{\mathrm{e}},$then 

$\mathrm{P}\left({\mathrm{D}}_{\mathrm{e}}\right|\mathrm{A}) = \frac{P\mathit{(}A\mathit{\backslash }D{}_{\mathit{e}}\mathit{)}P\mathit{(}D{}_{\mathit{e}}\mathit{)}}{P\mathit{\left(}A\mathit{\right)}}= \frac{P\mathit{(}A\mathit{\backslash }D{}_e\mathit{)}P\mathit{(}D{}_e\mathit{)}}{{\displaystyle \sum _{j\mathit{\in }J}}P\mathit{(}A\mathit{\backslash }D{}_{\mathrm{j}}\mathit{)}P\mathit{(}D{}_{\mathit{j}}\mathit{)}}$

References

1. Cancer Stat Facts: Prostate Cancer. Ref.: https://bit.ly/2jjAZO1 

2. Total population in the United States by gender from 2010 to 2024 (in millions). Ref.:https://bit.ly/2D6ayIa 

3. Lamothe, P. J. 2007. Reforma de los Estados Democráticos y de los Oclócratas. México: Primer Mandante Epistemócrata de los Estados Unidos Mexicanos.

4. Kasper DL, Fauci AS, Hause SL, et al. 2015. Harrison’s Principles of Internal Medicine. Ref.: https://bit.ly/2nQTsKg 

5. An Intuitive Explanation of Bayes' Theorem. Ref.: https://bit.ly/2o2vzz9 

6. Feynman R. 1965. The Character of Physical Law. Ref.: https://bit.ly/2oDeHiy 

7. Larroyo F. La Lógica de las Ciencias. 18ª ed. México: Editorial Porrúa; 1973.

8. Larroyo F. Filosofía de las Matemáticas. México: Editorial Porrúa. 1976.

9. Aleksandrov AD, Kolmogorov AN, y Lavrent’ev MA. 1969. Mathematics: Its Content, Methods and Meaning. Ref.: https://bit.ly/2o1gfmy 

10. Wittgenstein L. 1978. Observaciones Sobre los Fundamentos de la Matemática. Spain: Alianza Editorial. Ref.: https://bit.ly/2oDAS8g 

11. Illich I. 1975. Medical Nemesis: Expropriation of Health. United States: Random House. Ref.: https://bit.ly/2o0mEOR 

12. Larroyo F. Estudio Preliminar en Platón Diálogos. Mexíco: Editorial Porrúa. Colección Sepan Cuantos; 1996.

13. Ward Casscells BS, Arno Schoenberger MD, Thomas B, et al. 1978. Interpretation by Physicians of Clinical Laboratory Results. Ref.: https://bit.ly/2nRDmA2 

14. Teorema de Bayes. Ref.: https://bit.ly/2py480J 

15. Teorema de Bayes Problema 1. Estadística. Ref.: https://bit.ly/2nR0dvD 

16. Teorema de Bayes Problema 2. Estadística. Ref.: https://bit.ly/2n4Ym5J 

17. Teorema de Bayes. Problema 3. Estadística. Ref.: https://bit.ly/2py2xYM 

18. Papadakis M. A. y McPhee S. 2016. Current Medical Diagnose & Treatment. 55a Ed. USA: McGraw-Hill Education.

19. Epidemiology ch 01 07 Understanding Screening Tests. Ref.: https://bit.ly/2nRJ9FM 

20. Mark D. B. y Wong J. B. Decision–Making in Clinical Medicine en Kasper D. L, Fauci A. S, Hauser S. L, Longo D. L, Jameson J. L y Loscalzo J. Harrison’s Principles of Internal Medicine. 19a Ed. USA: McGraw-Hill Education; 2015. ISBN 978-0-07-180213-0.

21.Lann Cheuck, Prostate Cancer Diagnosis and Staging. 2019. Ref.: https://bit.ly/2n6jskl 

22. Laplace P. S. A.2009. Philosophical Essay on Probabilities. USA: Rough Draft.

23. Lamothe P. J. 2007. Por qué Yo No Debo Ser Presidente de México… Todavía. México: Primer Mandante Epistemócrata de los Estados Unidos Mexicanos.

24. Lamothe P. J. 1998. Epistemocracia: Primer Tratado General de Ingeniería Política. 2a Ed. México: Edamex.

25. Alexánderson E, Sierra C, y Lamothe P. A, 2008. Gated-Pet en Alexánderson E. y Meave A. Imagen Cardiovascular. México: Facultad de Medicina Universidad Nacional Autónoma de México.

26. Popper K. 2002. The Logic of Scientific Discovery. Routledge: Great Britain. Ref.: https://bit.ly/2o0RaYT 

27. Wilson, E. O. 199. Consilience. United States of America. Vintage.

28. Lamothe P, Baril B, Chi A, et al. 1981. Accessory Proteins for DNA Polymerase α Activity With Single-Strand DNA Templates. 78: 4723-4727. Ref.: https://bit.ly/2oB4HX3 

29. Lamothe P. 1992. Implicaciones Sociopoliticoeconómicas de la Ingeniería Genética. Anales Españoles de Pediatría. 36: 55-58.

30. Universidad abierta y a Distancia de México. Ref.: https://bit.ly/2n5aQKD 

31. Jeffrey RC. 2004. Subjective Probability: The Real Thing. New York. USA: Cambridge University Press. Ref.: https://bit.ly/2o4FBjt 

32. Jaynes E. T. 2003. Probability Theory: The Logic of Science. Cambridge. United Kingdom: The Press Syndicate of the University of Cambridge. Ref.: https://bit.ly/2n5MlwV 

33. Constitución de la OMS: principios. Ref.: https://bit.ly/1NUtfzq 

34. Pfeiffer P. E. Concepts of Probability Theory. USA: Dover Publications, Inc.; 1978.

35. Stone J. V. 2013.Bayes’ Rule: A Tutorial Introduction to Bayesian Analysis. USA: Sebtel Press. Ref.: https://bit.ly/2o4JJjt 

Download Provisional PDF Here