Welcome to International Journal of Biology and Medicine

Abstract

The purpose of this work is to provide evidence to the scientific community that there is solid scientific knowledge available to tame the pandemic, which is mainly a behavioral problem that requires cybernetics through behavioral engineering. Scientifically it is clear that the problem of the pandemic originates in human behavior and misinformation. Behavioral problems are addressed by cybernetics through behavioral engineering. Aristotelian causes of the pandemic are aberrant behavior. This is the field of battle and the obsession of the subject is the rise of the neurotransmitter dopamine. The question is not what is the probability that a patient with COVID-19 has a certain symptom or sign? Rather it is to calculate the probability that a patient with a certain sign or symptom has COVID-19. Without grasping the differential equations modeled by Kermack and McKendrick, it is impossible to have an idea of what is happening in the pandemic. Our straightforward theoretical approach is to use the wild unmodified SARS-CoV-2 to produce immunity by the simple expedient of diminishing the amount of the inoculum to the minimum minimorum. The problem with allowing people, deliberately attempting herd immunity, is that it has the dire effect that a high percentage will necessarily die. It is a matter of competence between two exponential functions. On one hand the exponential reproduction of the virus, and on the other hand, the exponential production of antibodies and activation of T cells. The aim is to diminish the amount of the inoculum to the minimum minimorum capable of infecting the minimum susceptible cell subpopulation. In this manner, herd immunity could be reached, which would allow a parsimonical response in the viral exponential growth that would not overwhelm the exponential immune response. It is expected that susceptible subjects could be infected in a variolation modality through the universal use of masks, maximizing the distance, rather than in a noregulated exposure of a putative low-risk segment of the population. In the logic of the decision, we must distinguish a desideratum from what is physically, economically, legally, and politically implementable. It is a matter of policy-making supported by science and law instead of doxastic logic based on misinformation and bigotry. It is a matter of policy enforcement by cybernetics, by behavior engineering, not of a recommendation. The guidelines, if they are to be implemented, depend on the application of cybernetics, and behavioral engineering. The apodictic inference from fallacies, in a doxastic and desiderative logic, is the origin of disinformation.

Keywords: COVID-19 Inoculum; Bayes Theorem; Cybernetics; Variolation; Herd immunity

Introduction

Epidemiologically, never is an adequate time to strive to be politically correct, even less in the presence of this pandemic. Scientists act based on science and law and not on beliefs, opinions, or rhetoric. Scientifically it is clear that the problem of the pandemic originates in human behavior, in the acquisition of the virus, in the dissemination and misinformation official, as well as in the media and on social networks [1]. Behavioral problems are addressed by cybernetics through behavioral engineering [2]. As in cases such as alcohol consumption, smoking, drugs, gun crimes, wars, sexually acquired diseases; the teleological Aristotelian causes are not tobacco, alcohol, drugs, and HIV, but aberrant behavior. The neural topography corresponds to the nucleus accumbens. This is the field of battle and the obsession of the subject is the rise of the neurotransmitter dopamine [3,4]. In every part of the world, the people are very demanding from their governments; but at the same time, they are tolerant with their own aberrant behavior against avoiding the dissemination of the SARS-CoV-2 [4,5].

Epidemiological Foundation

According to Bayes theorem (1763), the question is not what is the probability that a patient with COVID-19 has a certain symptom or sign? Rather it is to calculate the probability that a patient with a certain sign or symptom has COVID-19 [6,7].

If $\Delta =\{D_{\mathit{e}}:e\mathit{\in }J\mathit{\}}$ is any class of mutually exclusive countable events,

D_e = Disease
A = Abnormal result in the test
D _j= No disease
P( • ) = Bayesian Probability Function
If A is any abnormal test result with positive
such that A $\mathrm{A}\subset \underset{\mathrm{e}\in \mathrm{j}}{{\cup D}_{\mathrm{e}}}$ then:

$P\left(D{}_e|A\right) =\frac{P(A/D_e)P\left(D_e\right)}{P\left(A\right)}=\frac{P(A/D_e)P\left(D_e\right)}{{\displaystyle \sum _{j\in J}}P(A/D_j)P\left(D_j\right)}$

These are the deterministic differential equations of the epidemiological model developed by Kermack and McKendrick [8] that politicians, media communicators, and citizens genuinely concerned about COVID-19 should understand. Without grasping these differential equations, it is impossible to have an idea of what is happening in the pandemic:

$\frac{ds}{dt}=-\beta SI\sqrt{\frac{dl}{dt}=+\beta Sl-\gamma l\frac{dl}{dt}=\gamma l}$

$\frac{dS}{dt}+\frac{dI}{dt}+\frac{dR}{dt}=-\beta SI+\beta SI-\gamma I+\gamma l=0$

This is the paradigmatic classical model by which the growth rate of the pandemic can be estimated. It is based on three factors which are the susceptibility of subjects to be infected, the rate at which infections occur de facto (infectivity), and the rate of infection. The resistance includes those who recover and those who die. This is what constitutes the SIR model, which corresponds to the simultaneous solution of the three differential equations, as described in 1927 by W. O. Kermack and A. G. McKendrick [8]. 

The basic reproduction number R0 could be defined as the number of cases that we expect to occur, on average, in a homogeneous population, as a product of the infection caused by a single contagious individual, when the entire population is susceptible at the beginning of an epidemic before immunity begins to develop and before any attempt at immunization has been made. So, if a single person infects two others, then the R0 is 2 [8]. If the average R0 in the population is greater than 1, then the infection will spread according to the logistic function that initially grows exponentially. The model is tragically described obeying the following differential equation:

Where

N = Population
K = number of inhabitants that can be supported by the environment
r = population growth

$\frac{𝑑𝑁}{𝑑𝑡}=𝑟𝑁\left(1-\frac{N}{K}\right)$

$\frac{𝑑𝑁}{𝑑𝑡}=\frac{r}{K}N(K-N)$

$\frac{𝑑𝑁}{𝑑𝑡}=-\frac{r}{K}N(K-N)$

$\frac{1}{N(N-K)}dN=-\frac{r}{k}dt$

$\frac{1}{N(N-K)}dN=-\frac{r}{k}dt$

Integrating the two sides of the equation and solving for N

$𝑁(𝑡)=\frac{-KC{e}^{rt}}{1-C{e}^{rt}}$

$𝑁(𝑡)=\frac{KC}{\hspace{0.17em}C-e^{-rt}}$

$𝑁(𝑡)=\frac{K}{1-{\displaystyle \frac{{𝑒}^{-𝑟𝑡}}{C}}}$

When t=0,    N(0)=N_o

_{$C=\frac{N_o}{N_o-K}$}

_Substituting

_{$N\left(t\right)=\frac{K}{1+\left({\displaystyle \frac{N_o-K}{N_o}}-1\right)e^{-rt}}$}

$N\left(t\right)=\frac{K}{1+\left({\displaystyle \frac{K}{N_o}}-1\right)e^{-rt}}$

Behavioral foundations

If political correctness means accepting false data, axioms, premises, or protocol clauses and apodictically generating fallacious conclusions, then politically correctness consists in being against logic, mathematics, and the advances of science. It means incorporating hypostases rather than hypothesis, that everyone talks about but no one has demonstrated. It is possible to scientifically study everything, including beliefs, religion, free will, unconsciousness, qualia, etc, which is totally different from accepting that they exist. All the mentioned ones are incompatible with current scientific paradigms, in the same way, that the scientific study of schizophrenia; that is, not beginning with the acceptance that hallucinations correspond to reality; however, it is the case that the patients have them. A strategy to acquire herd immunity with the lowest mortality has been historically reached through vaccination. Notwithstanding there have been continuous naïve proponents with the wishful thinking of strategies to obtain herd immunity with low mortality. Classically, Viral vaccines are divided into attenuated live viruses, killed viruses, and viral fragments. However, there are alternatives to acquire immunity. Those alternatives are not a product of the sophisticated mind of the genius, they are the product of natural selection which by itself is a tragedy even though every living entity is a product of it. There could be an exception, a type of molecular anagnorisis: Variolation [9]. The differential equations of the Kermack and McKendrick model and its variants constitute the foundations upon which any epidemiological proposal related to the SARS-Cov-2 pandemic must be made. In the same way as the Kermack and McKendrick differential equations, the probabilitarian and Bayesian calculations must be rigorous, as well as the bimolecular, biological, immunological, and biophysical considerations.

Biophysics considerations

Biophysics determines the behavior of the virus after the release from the infected cell that possesses it, its expulsion, its dispersion and its trajectory in the air, its intraluminal behavior in the susceptible subject, and its interaction with the receptor [10].

Theoretical approach and purpose

Our straightforward theoretical approach is to use the wild unmodified SARS-CoV-2 to produce immunity by the simple expedient of diminishing the amount of the inoculum to the minimum minimorum. The purpose of this work is to provide evidence to the scientific community since there are various scientific disciplines actively involved in the COVID 19 pandemic in a systems theory approach, that there is solid scientific knowledge available to tame the pandemic, which is mainly a behavioral problem that requires cybernetics through behavioral engineering [2,11].

Desiderative considerations

While everybody is having a dream about the SARS-CoV-2 vaccine, a conundrum we face and we have to decide: Given the shortage of vaccines, what is going to be the assignation method? First of all, we have to recognize that once we have reached this point, the decision is going to be a violation of human rights. There are not going to be enough vaccines for everybody; at least, not at the beginning. Who gets the best vaccine? other decisions to be taken are: First in time then first in right (queue)?; By age?; To those who need the most (ad Lazarus fallacy); To the most necessary subjects for the society ( the ones we need the most); To the one who pays more (free market); Random aleatory, a type of lottery?; Will it be decided through a Plebiscite?; First the old people, women, and children?; First the workforce?; First the most exposed?; First, those to which the population is most exposed (the supermarket cashier for example)?.

Economical considerations

The economic considerations to provide protection according to priority for sectors of the market that are important like tobacco, alcohol beverages, bars, beauty parlors, fast food, casinos. They might be important in the economy but what they produce is not essential for the population, on the contrary, per se they could be hazardous. Faced with the scarcity of the vaccine and by a diversity of qualities, there will be a decision algorithm with which no one will agree, because those who want the vaccine, want it even if they do not deserve it, even if they are not the ones who need it the most, although not they are the ones who contribute the most to society, even if they do not have the right to have it. This is an existing conflict in spite of no one recognizing it, since the existence of reality is not subjected to a doxastic logic or a desiderative logic. Much less, the existence of the conflict is not conditionally subject to a process of ochlocratic suffrage [4]. The recent article: Genome wide Association Study of Severe Covid-19 with Respiratory Failure that appeared in The New England Journal of Medicine makes scientist, politicians, media commentators, and the public at large recognizing that some people, for genetic reasons, are at greater risk of making a serious clinical picture if they become infected. This fact immediately generates an inescapable violation of human rights due to discrimination. If these people are given preference then they are discriminated against by those who do not have the gene and if it is not given then they are discriminated against punishing them for genetic reasons [12]. If R0 is less than one, the infection will progress slowly and disappear. The higher the value of R0 the faster the epidemic will grow. The value of R0 is estimated from data obtained in the field, in other populations, or at other times and incorporated into the mathematical models. If the test has a sensitivity of 99% but a high number of patients are not tested and are considered negative, they are actually false negatives. False negatives are all those who, being ill, were not identified as such in the test, plus those who, being ill, were not tested and are reported as negative [4]. Now that more tests are done, the number of positives increases and the cause is twofold; On the one hand, patients previously asked by some states, to stay at home, unless they were seriously ill, are being subjected to the tests (one type of false negatives) and, dramatically due to ignorance of Bayes' theorem and the effect of false positives [4]. The fascination for the so-called herd immunity provokes a reckless, suicidal, and harmful social response against others. The proponents fallaciously assume that if the virus is allowed to spread in a controlled manner, the population will acquire sufficient immunity and spread will be prevented.

Exponential growth

The problem with letting people become infected spontaneously or worse, deliberately attempting herd immunity, is that it has the dire effect that a high percentage will necessarily die. This percentage is the fatality rate. Suppose hypothetically a viral disease that no one has acquired in the world. To do the exercise in a scandalous way for all critics, with elemental arithmetic: If R₀ = 1 or less and the incubation time is one week, 52 will be infected in one year. If R₀ = 2, then 2¹⁰, will be infected, approximately 1,000 (1,024), in 10 weeks and in 20 weeks, 10²⁰, approximately 1;000,000 will be infected and in 30 weeks 10³⁰ approximately 1,000;000,000 will be infected.

Since:

$\frac{(R_o-1)}{R_o}=1-\frac{1}{R_o}$

$R_o-1=R_o\left(1-\frac{1}{R_o}\right)$

$R_o-1=R_o-\frac{R_o}{R_o}$

$R_o-1=R_o-1$

To prevent the spread of infection, the proportion of the population that has to achieve immunity (Pi) has to be greater than 1- 1 / R0 which means greater than (R₀-1) / R0. For example, if R₀ = 2, then immunization needs to reach (2-1) / 2 = 50% of the population; however, if R₀ = 5, the proportion skyrockets to require (5-1) / 5 = 80% to be immune. Beyond this, an increase in R₀ of 10 increases the need to acquire an immunization of (10-1) / 10 = 90%. Measles has an R₀ that is greater than 10, for which it is necessary to immunize practically the entire population. Thus, if R₀ is 10, a child with measles will infect on average 10 healthy children if they are susceptible. If it turns out that other children have already been infected, then he will not be able to infect those who have died or those who are infected or those who have recovered. When the population's immunity has reached 90% or more, the chances of interacting with an unimmunized susceptible will tend to zero and the population will be immune, of course having paid with a death toll that the affected sadly cannot claim, which is the fatality rate. At any time, Re = R0 (1-Pi), where Pi, is the proportion of the population that is immune at that moment. These are the methods that involve the direct mathematical calculation of R0, which constitute the paradigm. Sensitivity depends, among other variables, on the time between exposure and performance of the test. Let us consider the prevalence of positivity in the RT PCR test. A virus can have a high fatality rate, but very low contagion. On the other hand, it can have a low fatality rate but be highly contagious. It is not only important to determine the probability of an outcome. It is much more important to consider the consequence of one result or the other. In Russian roulette the probability that the bullet hits is 1/5, which means that the probability that nothing happens is 4/5; that is, 80% probability in favor; however, 20% of those who calculate this way end up dead. What is worse, those who win the first time might feel good prognosticators and tend to repeat the bet until the bullet hits them. The case of Poliomyelitis is tragically illustrative in which we must separate the concept of infection from the sequel, which, according to the World Health Organization, the vast majority of poliovirus infections do not produce symptoms, but 5 to 10 out of 100 people infected with this virus may have some flu-like symptoms; however, 1 in 200 cases the virus destroys motor cells of the nervous system, causing permanent paralysis in the legs or arms. 30 years ago, polio paralyzed nearly 1,000 children every day [13]. Policymakers have to be aware that vaccines may not be efficient and may also have unexpected side effects. By the end of November 2020, there are about 1,500,000 deaths in the world attributable to COVID-19 and 63 million cases [14]. It is imperative to recognize that the ignorance of the concept of exponential growth has been considered the most extreme intellectual shortcoming in history [15-23]. As a Gedankenexperiment, (German: “thought experiment”) term used by Albert Einstein to describe his approach of using conceptual rather than actual experiments in creating the theory of relativity [24], theoretically, the ideal of our minimum minimorum approach would be to directly expose the minimum number of respiratory epithelial cells to the minimum number of particles of wild SARS-Cov-2. In this hypothetical hyperbolic scenario, the successful reproduction of the virus will provoke an immunological response. This response will be a parsimonious one i.e. not an overwhelming response. It will be in such a way that the immunological system will be able to mount an exponential response timely, which strictly will be superior to the exponential replication of the virus. If this can be achieved, we will have acquired not just an immunological solution against SARS-CoV-2, but against many past, present, and future pathogens, like HIV, Syphilis, etc. Some patients are HIV controllers [25]. Even though it is not known if those patients considered tolerant to HIV are cases produced by the exposure to a minimum minimorum inoculum, It would be consistent with our working Hypothesis. Why is the immunological response of a patient infected with 1,000 viral particles, different than that of a person infected with just one particle? The answer belongs to exponential growth [16-23]. The explanation is the behavior of the exponential functions. Let's suppose a hypothetical virus such that, once the virus is inside the cell, it can get replicated in one hour, so will have 2 viral particles, after 2 hours there will be 4 particles, after 3 later there will be 8 particles, and so on. If we continue this for 10 hours, we will have approximately 1,000 viral particles (1,024), and in 20 hours, 1;000,000 particles. The exponential function of antibody production and the exponential function of a T-cell activation will be higher than the exponential function of the virus reproduction. Now let’s suppose that a healthy patient gets in contact with a sick person with corona virus, in such a way that when this person gets infected, it happens not with one particle, but instead, with 1,000.

If a patient is infected with 1,000 viral particles they can get replicated in one hour, so there will be 2,000 viral particles, after 2 hours there will be 4,000 particles, after 3 hours there will be 8,000 particles, and so on. If we continue this for 10 hours we will have approximately 1;000,000 viral particles and in 20 hours, 1,000;000,000 particles. If the exponential growth of the immunological response outgrows the exponential growth of the virus replication, we have not just reached immunization, but we might have the solution to the Pandemic and to many that will follow. It is a matter of competence between two exponential functions. On one hand the exponential reproduction of the virus, and on the other hand, the exponential production of antibodies and activation of T cells. The aim is to diminish the amount of the inoculum to the minimum minimorum capable of infecting the minimum susceptible cell subpopulation in a susceptible person. The concept of the use of masks and contagion are intuitively described as a discrete phenomenon, even more so, Boolean, when in reality it is a continuous one, at least concerning the amount of inoculum. Not two patients receive the same amount of inoculum.

Immunological aspects

Theoretically, the key problem would be how to deliver the antigen in order to immunize the susceptible; that is, to find a way to get the minimum viral inoculum. In the article by Gandhi and Cols. and later in Perspective in NEJM [26]. They found the solution to the viral delivery problem. They proposed that the use of masks could diminish the inoculum and produce a less severe clinical picture. They described it pedagogically as variolation [9]. The use of face masks implemented universally would produce the desired effect of reducing the inoculum and, we hypothesized, consequently the parsimony of the exponential viral growth relative to the exponential growth of the immune response. It is a fundamental consideration to recognize that the amount of inoculum decays with the square of the distance between an infective person and the susceptible. In this regard, it is most illustrative: Exploring the impact of inoculum dose on host immunity and morbidity to inform model-based vaccine design [27].

Desiderative logic

Another recent publication related to this topic and pertinent to be judged contrasting against our hypothesis: The Great Barrington Declaration which is opposed to scientific knowledge [28]. The main arguments of the Great Barrington Declaration, all of them false or at least fallacious and also against human rights are: Current lockdown policies are producing devastating effects. Keeping students out of school is a grave injustice. We know that all populations will eventually reach herd immunity. The most compassionate approach that balances the risks and benefits of reaching herd immunity is to allow those who are at minimal risk of death to live their lives normally to build up immunity to the virus through natural infection, while better protecting those who are at highest risk. Those who are not vulnerable should immediately be allowed to resume life as normal. Schools and universities should be open to in-person teaching. Extracurricular activities, such as sports, should be resumed. Young low-risk adults should work normally, rather than from home. Restaurants and other businesses should open. Arts, music, sport, and other cultural activities should resume. People who are more at risk may participate if they wish, while society as a whole enjoys the protection conferred upon the vulnerable by those who have built up herd immunity. On October 4, 2020, Great Barrington, United States, The John Snow Memorandum [29] to which we epistemologically endorse appeared immediately. The publication of the Great Barrington Declaration is a dramatic example. Our conclusive recommended approach will improve the expected result of a policy that could wrongly be implemented based on the unscientific Great Barrington Declaration. Apart from the human rights of equality and non-discrimination, there are certain characteristics of some individuals that constitute assets for society and that society should take care of and protect, not because it is a genuine human right of those who possess these characteristics, but because it is a vital convenience for society and because the health and often the life of a large part of the population depends on the wellbeing of them. If the Great Barrington Declaration is enforced, we will have a Nash equilibrium in the worst of the conditions. Nash, John Forbes (1950) [30]. We are experiencing two simultaneous pandemics, one caused by SARS-Cov-2 and the other misinformation [1]. Great Barrington's statement sounds reasonable and seems to satisfy all parties, those who prefer to expose themselves, those who prefer to protect themselves, the economy, the government, the rulers. However, it has an undeniable rhetorical component. It is a praise of demagoguery. If attainable is going to be Nash equilibrium in non-Pareto optimal [30].

Doxastic considerations

Since it is easy for policies to be implemented based on appearance rather than in a scientific and legal foundation, we must consider that it is likely that policies derived from the Great Barrington declaration or on any analogous proposal will be generated that are implemented with tragic consequences, not only local but also national and global. Even in that absurd case, our proposal would lessen the severity of the tragic consequences.

Teleology and evolution of genes

Viruses and parasites, in general, have the tendency to explode, take over and hijack i.e. abduct the parasitized organisms, allowing them to multiply more or less successfully and modifying the behavior of the host improving the reproductive success of the parasite [31]. Most people do not believe in evolution. Among those who do, they do not understand it since they take the Lamarckian position. The exceptional Darwinian who believes in random variation and selection of the best fit are wrong because it is not survival but reproduction as can teach them the seductive male of the Mantis religiosa and the fertilizer of the black widow. The bottom concept lies in the selection of the genes, the selfish gene, which is the paradigm of evolution. What is inherited are the genes. What are selected are the genes and not the organisms [32].

Mathematical theory of games

In terms of the mathematical theory of games, it is detrimental for the virus to kill or incapacitate the parasitized organism, as this diminishes its multiplication success. It is inappropriate and naïve to consider SARS-Cov-2 as an enemy. With viruses, there is no possible peace agreement [30]. Other causes of possible failures of the Great Barrington declaration are that those who are exposed become infected and that they will later infect their protected relatives within their own homes; furthermore, we do not know the duration of immunity or its effectiveness. We think that those who expose themselves without face masks on the street are not very likely to wear face masks in their own homes, or to maintain the appropriate distance, etc., so as not to infect their high-risk relatives. The argument from the Great Barrington Declaration that herd immunity will eventually be achieved is fallacious, herd immunity for influence, HIV, syphilis, malaria, herpes, tuberculosis, and amebiasis has not been achieved. In spite of the fact that the Great Barrington Declaration has a clear shortcoming due to the possibility of intrafamilial contagious to fragile people from the infected. With the argument of protecting the elderly many old persons will be displaced to nursing homes. It is highly unlikely that the working young adult economical productive population will decide to live in the cellar to avoid transmitting the infections to the grandparents.

Probability applied to genetics

SARS-CoV-2 is a single-stranded RNA virus that is the longest known, it has 30,000 nucleotides, although the vast majority of mutations produce a disadvantage for the organism that suffers them, which is the case for any living organism, the rare mutations that accidentally confer advantage are the basis of the Darwinian selection. The duplication of the RNA genome of the SARS Co-2 virus has a very low error rate per reproductive cycle since it has the error-correcting enzymatic machinery. The lost time of presential education argument expressed in Great Barrington's statement is rhetorical and fallacious, on the contrary, it is the opportunity to show that current classroom education is a failure and not something that should be tried to maintain as a magnum opus. Confinement has allowed us to learn that we have to be selective; it is not a time when we should maintain our right to choose superfluous things or useless services. The misinformation pandemic has potentiated the expansion of the SARS-Cov-2 pandemic.

$$\begin{gathered} 𝑎: 𝑦=2^{𝑥} \\ 𝑏: 𝑦=4^{𝑥} \\ 𝑐: 𝑦={𝑒}^{𝑥} \\ 𝑑: 𝑦=\left(2^{𝑥}\right) \left(4^{𝑥}\right) \end{gathered}$$

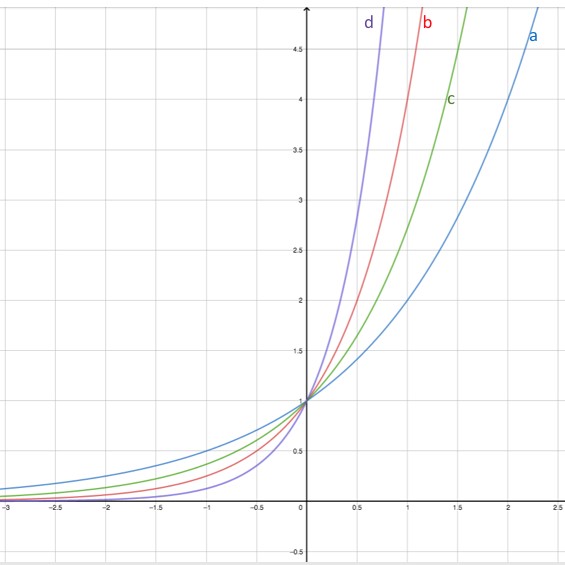
In this graphic, “c” represents the immunological response; “b” represents the exponential growth of the virus dominating the immune response; “a” represents the viral growth with minimal inoculum; “d” represents the multiplicative adverse effect of the growth of the virus multiplied by the effect of misinformation which increases the aberrant and irresponsible behavior [33]. So, when they are infected increases the probability that the susceptible will be infected but also increases the size of the inoculum, which increases the probability that if the interlocutor is infected he has a more serious clinical picture due to a larger inoculum. Thus, WhatsApp is better than the telephone to prevent and reduce the effect of SARS-Cov-2 because the interlocutors do not talk. Confinement has reduced environmental pollution, led to savings in transportation, a reduction in: accidents, fights, alcohol consumption, drugs, and sexual assaults.

Great Barrington's statement constitutes an ad verecundiam fallacy, as the signatories are not experts in what they propose. In a sense, it has a democratic tinge because it seems that everyone decides whether to expose or to protect themselves [4]. All of these considerations might apply to future pandemics as well. Many world-class experts incur the fallacy ad verecundiam, inferring on grounds that are beyond the area where they are experts. It is an instance of the Dunning–Kruger effect [34]. "Unskilled and Unaware of It: How Difficulties in Recognizing One's Own Incompetence lead to Inflated Self-Assessments". A scandalous instance is represented in the conference a scientist mistakenly conceives it in the Second Lecture in the COVID-19, SARS-CoV-2 and the Pandemic Series, presented by the MIT Department of Biology. Britt Glaunsinger of the University of California, Berkeley when she gave a talk titled "Corona virus Biology." She expressed: “If you have a genome that is 10,000 bases long, and the polymerase makes an error, on average, 1 in 10,000 you are going to have an error randomly somewhere every time you copy that RNA but if you have a longer genome you are going to have more than one error every time you copy that RNA”. The correct calculation is: The probability of having none errors would be [35,36].

${\left(\frac{9,999}{10,000}\right)}^{10,000}=0.368$

The probability of having at least 1 error is: $P=1-{\left(\frac{9,999}{10,000}\right)}^{10,000}=0.632$

It is physically unquestionable that If two people have face masks, the probability of contagion is the product of the independent probabilities. If the efficiency of the mask is: $\left(\frac{1}{\mathrm{t}}\right)$

When two interlocutors are wearing a mask the protector effect if one is contagious is: ${\left(\frac{1}{\mathrm{t}}\right)}^2$

The inoculum decays with the square of the distance between the infective and the susceptible. With the use of face masks, if an infective person interacts with a susceptible person, the probability of becoming infected as well as the amount of inoculum decreases, as it is the product of the independent probabilities of the protection that each face mask confers. The probability of contagion increases linearly with the time of exposure. We hypothesize that since children spend more time at a large distance from their peers, they stayed less time in close contact with each other, they spent more time outdoors, and probably, due to those causes, the infected children acquire the infection with smaller inoculum than adults. This would be compatible with our hypothesis that with less inoculum, we are to expect more subclinical cases and less clinical manifestations with the consequent lesser mortality. Even though our recommendations are far from ideal they could improve almost any policy in confronting the pandemic. This includes the implementation, against our will, of the Great Barrington Declaration. Our model applies equally to any present or future epidemic/pandemic. We must keep in mind that the cost to obtain herd immunity is determined by the lethality. As per November 29, 2020, According to MORTALITY ANALYSES from coronavirus resource Center of Johns Hopkins University & Medicine, the number of deaths per 100 confirmed cases (observed case-fatality ratio) the highest in the world is for Mexico with 9.6% and 2.0% for the United States. This means that grosso modo (roughly), if we let the pandemic grow without bound we could expect 9.6% of the Mexican population to die and 2.0 % of the US population to die. So, it would be 10 million deaths in Mexico and 6 million in the United States. According to our World in Data The case fatality rate for Mexico is 10%, while for the USA and for the World is slightly above 2.5% [37].

Cybernetics and behavioral engineering

In the logic of the decision, we must distinguish a desideratum from what is physically, economically, legally, and politically implementable. It is a matter of policy-making supported by science and law instead of doxastic logic based on misinformation and bigotry. It is a matter of policy enforcement by cybernetics, by behavior engineering, not of a recommendation [38]. The Director-General of the World Health Organization (WHO), Tedros Adhanom Ghebreyesus expressed at the Munich Security Conference: “But we’re not just fighting an epidemic; we’re fighting an infodemic” [1,39]. We have to decide whether to protect the vulnerable versus protecting the best and brightest genius minds of our society, those most transcendent to the world i.e. the clinicians and the researchers, the medical personnel, the epidemiologists, telemedicine and educational communications engineering staff, etc. Although everyone has the same rights, each person's contribution to the well-being and health of society is different. The physician and the one who is irresponsibly and voluntarily exposed to SARS-Cov-2 have the same rights; however, one is a benefactor and the other is a member of the society who has a behavior with potentially adverse consequences for others which is not only inadmissible, but many countries consider a crime to spread an infection knowing that one is sick of a contagious disease. Also, those who can educate without exposing the students, distance learning, virtual education as is the case of Khan Academy, MITx, Coursera, That Quiz, or at individual producers like us. We have a channel on YouTube: Principia Pedagógica Eléntica Heuristic. No school, no teachers! 4000 scientific lessons. This is more than what an average Bachelor's degree graduate could expect to learn in the best universities of the world [40]. There is no gun, no cigarette, no saturated fatty acid, no illicit drug, no torture, no discrimination act, and no education act through punishment that can be considered healthy. In the same way, there is no exotic pet, an exotic meal, hunting of exotic animals, zoophilia that may be accepted as appropriate for health. We maintain that this extends to the fact that domestic animals are not healthy for global health, even if they are perceived as part of the family and if they are considered cute. Already, the first case of SARS-CoV-2 in mink has been confirmed in Oregon in The United States, res ipsa loquitur [41]. We cannot ignore the fact that our invasion of other mammalian habitats and bizarre behavior has been a substantial component of the SARS-Cov-2 and HIV tragedies. We cannot think about vaccination without considering Edward Jenner’s discoveries [42].

Extracted from

An Inquiry into the Causes and Effects of the Variolæ Vaccine, Or Cow-Pox. 1798 Jenner, Edward. The Three Original Publications on Vaccination against Smallpox [42]. The deviation of man from the state in which he was originally placed by nature seems to have proved to him a prolific source of diseases. I selected a healthy boy, about eight years old, for the purpose of inoculation for the cow-pox. The matter was taken from a sore on the hand of a dairymaid, who was infected by her master’s cows, and it was inserted, into the arm of the boy by means of two superficial incisions. On the seventh day, he complained of uneasiness in the axilla, and on the ninth, he became a little chilly, lost his appetite, and had a slight headache. During the whole of this day, he was perceptibly indisposed and spent the night with some degree of restlessness, but on the day following he was perfectly well. In order to ascertain whether the boy was secure from the contagion of the smallpox, he was inoculated with variolous matter, taken from a pustule. Several slight punctures and incisions were made and the matter was carefully inserted, but no disease followed. Several months afterwards he was again inoculated with variolous matter, but no sensible effect was produced on the constitution.

We would like to share our thoughts with the reader: What would our present society do to Jenner if he would have done his experiments today? What do we learn from Jenner’s actions? What would we consider pertinent to teach Jenner scientifically and ethically?.

Conclusion

People who want to go out run the risk of getting infected. Our proposal is the cheapest and simplest. It is intuitive to think that the greater the inoculum, the greater the probability of becoming infected, which is fully recognized. However, larger inoculum tend to progress to more serious clinical pictures which is something that almost nobody considers. Not only in this pandemic but also in those that will follow soon, as these will arrive more and more frequently if we continue to fail to comply with what we propose in this article. One concept that is fundamental and that is practically never considered is that preventive medicine and healthcare medicine increase the prevalence of many diseases, which is a well-known epidemiological phenomenon and that is also contrary to what the World Health Organization proposes: to seek the greatest biopsychosocial benefit for most of the world. This is an instance of the fallacy of composition. We are not saying that it should not be done, we have demonstrated that the WHO definition has to change from an inspirational policy to an achievable result. Since according to the CONSTITUTION OF THE WORLD HEALTH ORGANIZATION: Health is a state of complete physical, mental, and social well-being and not merely the absence of disease or infirmity. Thus, the conclusion: Res ipsa loquitur (words speak by themselves). These are the social costs to pay for tame anti-scientific doxastic logic and the pandemic. The behavior engineering optimization goal is going to be through the universal use of approved mask, do not deal with travelers, do not deal with those who are exposed; that is, with those who do not comply with this list, do not deal with those who have clinical manifestations, do not share cutlery or glasses, cover your mouth when coughing, do not attend weddings or wakes, do not get on busses or planes, pay everything online, do not carry out or tolerate, encourage or allow useless commercial, cultural, entertainment activity; but only the essentials of the market, fewer hairdressers, gyms, etc., no face-to-face activity in schools, businesses, or procedures, do not travel uselessly, permanent and universal application of cybernetics, radical behaviorism and Bayes' theorem application in every conditional probability decision, recognize the false suffrage ochlocracy. All this translates into a low probability of becoming infected, but also in low inoculum. Patients with subclinical clinical pictures release fewer viruses. The greatest distance, the shortest interaction time, and no gathering. Continuous use of masks, do not eat together since it is a moment in which we remove the masks, eat alone and isolated, do not go to cinemas, restaurants, bars, do not go out, have all the meetings outdoors, with fewer people, no meetings, wash hands continuously, no shouting, no singing, no talking, no kissing, no touching. Not doing things without sense. Make the period an opportunity to learn logic, mathematics, physics, chemistry, biology, physiology, computation science are fields pursuable during the confinement. It is tragic that the reason to open an unnecessary business is not that it is advantageous for society but because those who sell the superfluous need the money and that money will be used to demand other products and services. Economics is an instance of thermodynamics and as such has to be approached [43,44].

Corollary

The guidelines, if they are to be implemented, depend on the application of cybernetics, radical behaviorism, and the behavioral engineering that derives from it. Inoculum decays with the square of the distance and linearly with the exposure time. If universal mask usage is enforced, whenever two persons, one of whom has been susceptible and the other has been contagious, the protector effect is the product of both of them. Thus, if the mask reduces the amount of virus to 1/10, then when both are wearing them, the reduction is to 1/10 times 1/10, so it is 1/100. These diminish the probability of infection to 1/100, but also, and fundamentally pertinent for our proposition is that, in case of contagious, the inoculum would tend to be 1/100 of what would have been without any mask. All this translates into a low probability of becoming infected, but also in low inoculum. Patients with subclinical disease release fewer viruses. The greatest distance, the shortest interaction time, and no gathering. Continuous use of masks, do not eat together since it is a moment in which we remove the masks, eat alone and isolated, do not go to cinemas, restaurants, bars, do not go out, have all the meetings outdoors, with fewer people, no meetings, wash hands continuously, no shouting, no singing, no talking, no kissing, no touching. Not doing things without sense. Make this tragic period an opportunity to learn logic, mathematics, physics, chemistry, biology, physiology, computation science are fields pursuable during the confinement [6,38].

Possible Conflict of Interest

Nery Lamothe and Mara Lamothe have received official communication from The Mexican Secretaria de Gobernación, Number DACCP-CG/294/19 and dated 29 November 2019, related to the donation of 650 University Lessons to the Government of the Mexican Republic and to become advisors to the President of Mexico in Mathematics and Science. For the aforementioned reasons, this work is dedicated to the Mexican citizens, represented constitutionally by President Lic. Andrés Manuel López Obrador.

References

1. Shannon C. 1949. The Mathematical Theory of Communication. USA.
2. Skinner BF. 1974. About Behaviorism. USA. Vintage Books.
3. Aristoteles. 1987. Tratados de Lógica. México. Editorial Porrúa
4. Lamothe PJ. 2007. Reforma de los Estados Democráticos y de los Oclócratas. México: Primer Mandante Epistemócrata de los Estados Unidos Mexicanos.
5. Wiener N. 1961. Cybernetics Or Control and Communication in the Animal and the Machine. MIT. Ref.: https://pubmed.ncbi.nlm.nih.gov/31828533/  
6. Bayes Mr, Price Mr. 1763. An Essay towards Solving a Problem in the Doctrine of Chances. By the Late Rev. Mr. Bayes, F. R. S. Communicated by Mr. Price, in a Letter to John Canton, A. M. F. R. S. Philosophical Transactions of the Royal Society of London. 53: 370-418.
7. Mark DBy, Wong JB, en Jameson J, et al. 2020. Harrison’s Principles of Internal Medicine. 19a Ed. USA: McGraw-Hill Education.
8. Kermack WO, McKendrick AG. 1927. A contribution to the mathematical theory of epidemics. The Royal Society.
9. Gandhi M. Rutherford GW. 2020. Facial Masking for Covid-19-Potential for “Variolation” as We Await a Vaccine. Ref.: https://pubmed.ncbi.nlm.nih.gov/32897661/  
10. Herman IP. Physics of the Human Body. Springer
11. Lamothe PJ. 1998. Epistemocracia: Primer tratado general de ingeniería política. 2a Ed. México: Edamex.
12. Franke A, Bujanda L, Buti M, et al. The Severe Covid-19 GWAS Group.
Genomewide Association Study of Severe Covid-19 with Respiratory Failure. 2020. New England Journal of Medicine. Ref.: https://pubmed.ncbi.nlm.nih.gov/32558485/  
13. World Health Organization. Polio eradication. 2018.
14. Coronavirus Resource Center. 2020 by Johns Hopkins University & Medicine. Ref.: https://pubmed.ncbi.nlm.nih.gov/32754041/  
15. Bartlett AA. Exponential Growth Arithmetic, Population and Energy.
16. Lamothe N. Lamothe M. 2020. COVID-19. El Presidente Tiene que Enseñarle a los Mexicanos a Contar con los Dedos. Principia Pedagógica Eléntica Heurística.
17. Lamothe N, Lamothe M. 2020. Modelo Crecimiento Exponencial Población. Introducción. Principia Pedagógica Eléntica Heurística.
18. Lamothe N, Lamothe M. 2020. Ecuación Logística. Crecimiento Poblacional. Principia Pedagógica Eléntica Heurística.
19. Lamothe N, Lamothe M. 2020. Ecuación Logística. Límite cuando el tiempo tiende a infinito. Crecimiento Población. Principia Pedagógica Eléntica Heurística.
20. Lamothe N, Lamothe M. 2020. Para Entender la Pandemia del COVID-19 Hay que Estar Preparados. Ecuación Logística. Principia Pedagógica Eléntica Heurística.
21. Lamothe N, Lamothe M. 2014. Área Ocupada por Lirios en una Laguna. Problema (1/3). Función Exponencial. Principia Pedagógica Eléntica Heurística.
22. Lamothe N, Lamothe M. 2014. Área Ocupada por Lirios en una Laguna. Problema (2/3). Función Exponencial. Principia Pedagógica Eléntica Heurística.
23. Lamothe N, Lamothe M. 2014. Área Ocupada por Lirios en una Laguna. Problema (3/3). Función Exponencial. Principia Pedagógica Eléntica Heurística.
24. Sidney Perkowitz. 2010. Gedankenexperiment. Encyclopædia Britannica. https://www.britannica.com/science/Gedankenexperiment  
25. Noël N, Saez-Cirion A, Avettand-Fenoël V, et al. 2019. HIV controllers: to treat or not to treat? Is that the right question? 6: 1878-1884:
26. Gandhi M, Beyrer C, Goosby E. 2020. Masks Do More Than Protect Others During COVID-19: Reducing the Inoculum of SARS-CoV-2 to Protect the Wearer. J GEN INTERN MED. 35: 3063-3066. Ref.: https://pubmed.ncbi.nlm.nih.gov/32737790/  
27. Handel A. 2018. Exploring the impact of inoculum dose on host immunity and morbidity to inform model-based vaccine design. National Center of Biotechnology Information. Ref.: https://pubmed.ncbi.nlm.nih.gov/30273336/ 
28. Kulldorff M, Kavaliunas A, Bhattacharya Y. 2020. The Great Barrington Declaration.
29. John Snow Memorandum.
30. Nash, John Forbes. 1950. The Bargaining Problem. Econometrica. Econometric Society. 18: 155-162.
31. Burt A, Trivers R. 2006. Genes in Conflict. USA. Belknap Harvard.
32. Dawkins R. 1982. The Extended Phenotype. Great Britain. Oxford.
33. Barreda S, Asadi S, Cappa CD. et al. The Impact of Vocalization Loudness on COVID-19 Transmission in Indoor Spaces.
34. Kruger J, Dunning D. 1999. Unskilled and Unaware of It: How Difficulties in Recognizing One's Own Incompetence lead to Inflated Self-Assessments. Journal of Personality and Social Psychology. 77: 1121-1134. Ref.: https://pubmed.ncbi.nlm.nih.gov/10626367/  
35. Glaunsinger B. 2020. Lecture 2: Coronavirus biology. 36. Jaynes ET. 2003. Probability Theory: The Logic of Science. Cambridge. United Kingdom: The Press Syndicate of the University of Cambridge.
37. Hannah Ritchie, Esteban Ortiz-Ospina, Diana Beltekian, et al. 2020. Mortality Risk of COVID-19. USA. our World in Data.
38. Jeffrey RC. 1965. The Logic of Decision. 2 Ed. USA. The Univerity of Chicago.
39. Adhanom T. 2020. Munich Security Conference. World Health Organization.
40. Lamothe N, Lamothe M. Principia Pedagógica Eléntica Heurística. Ref.: https://pubmed.ncbi.nlm.nih.gov/29193948/  
41. Oregon Department of Agriculture2020. First case of SARS-CoV-2 in mink confirmed in Oregon.
42. Jenner, Edward. 2001. The Three Original Publications on Vaccination Against Smallpox. Vol. XXXVIII, Part 4. The Harvard Classics. New York: P.F. Collier & Son. 1909-1914. Bartleby.com.
43. World Health Organization. 2020. CONSTITUTION OF THE WORLD HEALTH ORGANIZATION THE STATES. USA. 45. 44. Georgescu-Roegen N. 1976. Energy and Economic Myths. USA. Pergamon.

Download Provisional PDF Here